в частности, для одномерной задачи прямолинейно-параллельного движения жидкости (фильтрация к дренажной галерее или от нее) уравнение (3.3) принимает вид основного уравнения (3.1). Уравнение (3.3) впервые было получено в работе [20].

3.3. Прямое применение анализа размерностей

в модифицированной задаче о мгновенном тепловом источнике

Попробуем теперь найти решение задачи о мгновенном отборе из малой области упруго-пластического пласта конечной массы жидкости. Казалось бы, получение этого решения сводится ввиду лпнейной зависимости плотности жидкости от ее давления к построению решения задачи типа мгновенного точечного источника для уравнения (3.1). Мы попытаемся построить такое решение при помощи анализа размерности, но дальнейший анализ покажет, что в действительности дело обстоит сложнее. Итак, ищется решение уравнения (3.1), удовлетворяющее начальному условию и условию на бесконечности

и{х, 0) = 0 при д::50; J и{х, 0)dx==Q; ы(±оо, 0=0. (3.4)

- со

Как хорошо известно и уже отмечалось выше, для случая XI = % (классическое уравнение теплопроводности, фильтрация в упругой пористой среде) такое решение существует, автомо-дельно и представляется в виде (2.16). Казалось бы, соображения анализа размерности при Улфп должны проходить совершенно так же, как и в случае ki = х, поскольку список определяющих параметров в модифицированной задаче дополняется по сравнению с классической задачей о мгновенном тепловом источнике только безразмерным постоянным параметром е = щ/к. На первый взгляд, следовательно, искомое решение должно представляться в виде

u = (Q )ф{l, 8); 1 = х/, (3.5)

причем функция Ф - непрерывная с непрерывной производной по I и четная, Ф(-е) =Ф(, г). Для области нагружения (dtu 0) в силу автомодельности задачи должно быть

\x\Xo{t)loKt,

где go -постоянная, зависящая от е; для области разгрузки

0<\x\Xo{t),

Однако при щфус решения уравнения (3.1) в форме (3.5), непрерывного и обладающего непрерывной производной по х (непрерывность потока жидкости) и удовлетворяющего естественным условиям симметрии и обращения в нуль на бесконечности, не су-

ществует. Чтобы в этом убедиться, подставим (3.5) в уравнение (3.1) и получим для Ф обыкновенное уравнение с разрывным коэффициентом при старшей производной

причем точка = 5о соответствует обращению в нуль величины d(gO)/dg, которой, как легко получить из (3.5), пропорциональна производная dtU. Интегрируя, находим:

dl 2

~Ф = 1 при 0<£<о;

+4-Ф = 2 при Ho<UI<oo. (3.7)

В силу симметрии и отсутствия притока при л: = 0 в моменты >0 dO/dl = 0 при gO; при loo стремится к нулю функция 1Ф (суммарное колиство отобранной жидкости в каждый момент конечно и функциями должна быть интегрируемой). Отсюда 1 = 62 = 0. Интегрируя предыдущие уравнения, получаем:

ф = Сзехр(-Н2/48) при 0<U<o;

Ф = С4ехр(-2/4) при o<UI<, (3.8)

где сз и С4 -новые константы. Условия непрерывности функции и {х, t) и ее производной по х приводят к требованию непрерывности Ф и dO/dl при g = b откуда и из предыдущих уравнений получается линейная система однородных алгебраических уравнений для определения сз и Ci,:

cs exp (-о/4е) = ехр (-о/4);

Сг (Уг) ехр (-Ео/4е) = До ехр (-Л). (3.9)

При гф1, т. е. при щфк, эта система, очевидно, не имеет нетривиального решений ни при каком конечном go, поскольку ее определитель отличен от нуля. Тем самым доказано, что решения поставленной задачи в виде (3.5) не существует: тривиальное решение, очевидно, не удовлетворяет начальному условию (3.4).

3.4. Численный эксперимент. Автомодельная промежуточная асимптотика

Для того чтобы разобраться в возникшем парадоксе, обратимся к результатам численного эксперимента Ч Уравнение (3.1) интегрировалось при различных начальных условиях для разных значений параметра 8=xi/x. Начальные условия (3.4) представ-

Численные расчеты были выполнены В. М. Уроевым.

ляются обобщенной функцией и непосредственно в машинный счет заложены быть не могут. Поэтому они имитировались различными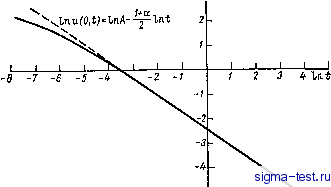

Рис. 3.1. Закон затухания максимума функции и(х, t) быстро становится степенным.

u(x,t)m/A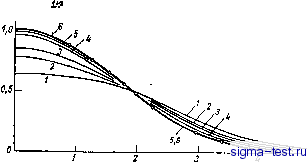

Рис. 3.2. Выход на автомодельную промежуточную асимптотику решения неавтомодельной начальной задачи для уравнения (3.1) при 8=2 и начальных данных 0) = 10 (0л:0,1)> и{х, 0)=0(jc>0,l).

/) =0,001; 2) =0,002; 3) =0,003; 4) =0.015; 5) /=0,040; 6) < 0,225.

сосредоточенными в малой, но конечной области вблизи л: = О, начальными распределениями и{х, 0), например,

гг(д:, 0) = 10 при -0,1<д:<0,1;

u{x,0)=Q при 0,1<д:<оо.

Результаты численного эксперимента получились весьма показательными. Прежде всего оказалось, что закон затухания величины а (О, t)-максимума функции и{х, t)-быстро становится