уравнение, должно выполняться условие v = [i = Я/2, так что автомодельная предельная форма решения при ц-О представляется в отличие от (12.48) в виде

b = AH-f{l); l = zlAt-\ l = aAt-, (12.57)

где Л, а - постоянные, причем [Л]=LГ~*+, а а - безразмерная величина. Очевидно, что параметр [i из анализа размерности определить нельзя.

Функция f удовлетворяет уравнению

{d/dl) (а Vf df/dl) + (1 - ) Е df/dl + 2ixf - cfya = 0. (12.58)

Легко показать, что, как и в предположении полной автомодельности (а = 0), все решения этого уравнения, не обраш.аюш.иеся в бесконечность при g-cx), непрерывные с непрерывной величиной л/f df/dl (что вытекает из требования непрерывности турбулентной энергии и ее потока) на самом деле обраш.аются в тождественный нуль начиная с некоторой точки g = go>0. В точке g = go обраш.ается в нуль величина безразмерного потока турбулентной энергии (л/f df/dl) 1=1,-оу так как при 1>1о эта величина

тождественно равна нулю. Действительно, при малых f последний член левой части (12.58) мал сравнительно с предыдущим и им можно пренебречь. Для получающегося при этом укороченного уравнения сформулированный результат известен [4, 17] (ср. ниже, а также главу 2).

Таким образом, глубина турбулизованной области, как и в предположении полной автомодельности, получается в каждый момент конечной. Она определяется соотношением

h = loAt-. (12.59)

Суммарная турбулентная энергия в турбулизованной области меняется со временем, согласно (12.57) и (12.59), по закону

\bdz = A4- \f{l)dlt-, (12.60)

и интегральная скорость диссипации уже также зависит от времени:

\dz=t-\flr. (12.61)

о о

Таким образом, отличие от случая полной автомодельности оказалось количественным, но не качественным: при обоих предположениях глубина турбулизованной области в каждый момент оказалась конечной.

Проведенный анализ показывает, что предположение о бесконечной глубине верхнего слоя было излишним: ввиду конечной ско-

рости распространения турбулентного фронта конечность глубины слоя не будет сказываться вплоть до достижения турбулентным фронтом границы раздела слоев. Анализ показал также, что масштаб турбулентности составляет определенную долю a/go глубины турбулизованной области.

5. Распространение внутренних гравитационных волн вблизи границы раздела слоев тяжелой и легкой жидкостей (рис. 12.4) определяется обычной потенциальной теорией. На стационарную картину волн, распространяющихся по границе раздела слоев, турбулентность не оказывает влияния, пока фронт турбулентности не войдет в непосредственную окрестность границы раздела слоев. Дело в том, что поле скоростей волнового движения быстро (экспо-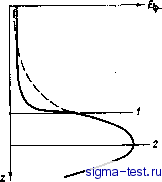

Рис. 12.8. Перераспределение волновой энергии по всему объему турбулизованной области.

/ - фронт турбулентности, 2 -

граница раздела слоев,

ненциально) затухает по обе стороны поверхности раздела слоев. Наличие турбулентности приводит к тому, что возникает турбулентный поток j энергии потенциального волнового движения (см. работу А. Ю. Бенилова [27]), направленный против ее градиента:

j = -фgrad£ф, (12.62)

где /Сф - коэффициент турбулентного обмена волновой энергии, который вводится так же, как ранее вводились аналогичные коэффициенты обмена массы, импульса и т. д. Применяя гипотезу автомодельности А. Н. Колмогорова, мы считаем этот коэффициент пропорциональным коэффициенту обмена импульса турбулентной энергии, так что Кц)1л/Ь .

До прихода турбулентности в области больших градиентов ф,

т. е. вблизи границы раздела, коэффициент KtlJb равен нулю, так как равна нулю турбулентная энергия. Пока фронт турбулентности далек от границы раздела, градиент волновой энергии егаёЯф в области, охваченной турбулентностью, экспоненциально мал, поэтому турбулентный поток волновой энергии мал везде. Когда же фронт турбулентности подходит к границе раздела слоев,

коэффициент обмена Kl/b там становится отличным от нуля, и, поскольку вблизи границы раздела gvdiAE не мал, возникает

турбулентный поток волновой энергии (рис. 12.8). Из-за этого потока волновая энергия распределяется более или менее равномерно по всему верхнему слою. Таким образом, как только фронт турбулентности захватит поверхность раздела слоев, действие вол-нопродуктора становится неэффективным: энергия волн благодаря турбулентности распределяется по всему объему сосуда, а не сосредотачивается вблизи, поверхности раздела, как это было в отсутствии турбулентности. Это и приводит к выглаживанию волн на поверхности раздела.

Разумеется, частный характер рассмотренной здесь геометрии явления несуш,ествен. Мы столкнулись при анализе опыта Филлипса с явлением совершенно общего характера: турбулентное образование, распространяющееся в жидкости и ограниченное при малой фоновой турбулентности резким фронтом, набегая на область, охваченную нетурбулентным волновым движением, всасывает в себя энергию волнового движения и тем самым выглаживает волны. Это явление могут наблюдать, например, катающиеся на водных лыжак: за глиссером образуется гладкая дорожка из-за того, что турбулентная спутная струя глиссера всасывает в себя энергию волн. Однако, стоя на этой дорожке лыжник испытывает частые слабые толчки, обусловленные турбулентностью.

Отметим, что основной для проведенного рассмотрения примечательный факт наличия резкой границы турбулизованной и нетур-булизованной областей, полученный здесь теоретически, неоднократно отмечался экспериментаторами (см. особенно статью Л. Коваснаи и др. [156] и монографию Дж. Тернера [208], в которых можно найти также обзор более ранних работ).

6. Сделаем несколько замечаний. В соотношениях (12.57) можно нормировать функцию / произвольно, при этом могут изменяться только постоянные А и а. Поэтому нормируем решение уравнения (12.58) условием

(aVfrff/4)=o=-l, (12.63)

совпадающим с первым условием (12.50), причем второе условие (12.50), т. е. f{oo) = О, тоже остается в силе. Таким образом, при заданном а, которое при рассматриваемом подходе не определяется и должно находиться из более подробной теории или опыта, нужное нам решение уравнения (12.58) однозначно определяется единственным параметром [х. Для нахождения параметра р, необходимо поставить задачу на собственные значения.

Рассмотрим простейший возможный вариант постановки этой задачи. Решение (12.57) при z = 0 дает с учетом нормировочного условия (12.63) для притока энергии на границе

так что приток энергии от решетки со временем убывает. Нетрудно дать этому физическое истолкование. В отличие от поступательно движущейся внутрь жидкости сплошной пластинки (например, штампа конечных размеров на плоской границе жидкости), которая передает жидкости определенную порцию энергии, заставляя ее двигаться перед собой, в решетке имеются сквозные отверстия.