перемещениями типа ёх, ёу, ez, так и углобыми неремещениями оси OS, которые будем характеризовать д/умя углами поворота аир относительно осей 0V и соответственно (рис. 20, б).

Условимся в дальнейшем рассматривать лишь малые смещения. Тогда зазор между несущими поверхностями можно представить в виде

h = Л + тосг + (А/1)угл + (3.30)

Здесь ho = ho (ф, z) -зазор при несмещенном положении шипа; (Л)пост (/1)угл -независимые вариации зазора, соответствую-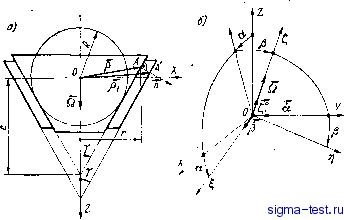

Рис.;20

щие поступательным (рассмотрены в п. 12) и угловым смещениям. шипа относительно подшипника.

Учитывая только угловые смещения шипа, составим векторное уравнение (рис. 20, а)

р1 = P + n/i>

(3.31)

где р и pi -радиус-векторы точекЛ и А, расположенных на поверхностях шипа и подшипника соответственно {АА = h);

п - орт нормали к поверхности шипа. Выразим эти векторы через их составляющие по координатным осям, пометив орты осей индексом нуль:

Р = + -ri +1% р, = hx, + YY, + Z%; (3.32)

n = I cos Y COS Ф + r cos 7 sin Ф + sin y. (3.33)

Угловая координата ф отсчитывается вдоль окружности шипа по оси t,.

Заметим,что при отсутствии поступательного смещения шипа нет необходимости делать различие между системами координат 82 .

OXYZ и OiXiYiZi. Тогда, рассматривая поворот оси шипа как ортогональное преобразование трехмерного векторного пространства и ограничиваясь лишь малыми углами поворота а, Р (рис. 20, б), при которых cos а cos\P 1; sin а а; sin р р, представим уравнение (3.31) с учетом (3.32) и (3.33) в виде

/cosy cos ф

1 О а\ О 1 р \ а р и

Согласно рис. 20, а:

l = rc6s(p{ Т1 = г51пф; = с -rctgy.

cos Y sin ф siny

(3.34)

(3.35)

где с = R CSC у.

Искомое выражение для h можно получить, подставляя X, Y, Z из (3.34) в следующее уравнение поверхности подшипника:

X + 1 = (Z-)ngY

(3.36)

Для определения (А/1)угл достаточно ограничиться уравнениями в вариациях. Варьируя уравнения (3.34) и (3.36) и отбрасывая малые члены, содержащие множители а {Ah)y , Р (Щул, /JqAz, hfpi., /loP, получим:

lAX-\-y]AY=g-c)tgyAZ;

АХ =! -f- {Ah)yj,cos у cos ф;

AF gp + (А/1)угл cos у sin ф; AZ - - TiP + (А/1)урл sin Y. ,

(3.37)

Отсюда с учетом (3.35) находим выражение вариации зазора, обусловленной угловыми перемещениями шипа в коническом подшипнике,

(A/i)y, {г sin Y - g cos у) (а cos ф + р sin ф). (3.38)

Из (3.38)-как частные случаи получаем вариации зазоров:

1) для цилиндрического подшипника (Y -* 0)

(А/1)у,л (а .cos ф + Р sin ф); (3.39)

2) для плоского упорного подшипника (у-)

(А/1)угл г (а cos ф + р sin ф). (3.40)

Формулы (3.38)-(3.40) позволяют найТи добавочные члены выражений (3.29), (3.21) и (3.23), которые определяют толщину смазочного слоя в опорах различной геометрии без учета перекоса осей шипа и подшипника.

6* . 83

14. К вопросу о выборе метода решения краевых задач газовой сказки

Решение краевых задач газовой смазки связано со значительными трудностями, которые обусловлены, прежде всего, нелинейностью уравнения Рейнольдса. Наиболее высокая точность решения таких задач может быть получена численным интегрированием с помощью ЭВМ (см. п. 2), однако этот способ часто оказывается дорогостоящим для массовых расчетов и неудобным в инженерной практике.

Наряду с численными методами, к решению задач газовой смазки применяют приближенные аналитические методы, среди которых, выделяют метод возмущений и его модификацию (метод РЯ-линеаризации Османа [53, т. 83, № 2]).

Метод РЯ-линеаризации привлекает к себе внимание благодаря его простоте и результативности. Сопоставление статических и динамических характеристик простого цилиндрического подшип- ника, рассчитанных на основании этого метода, с результатами других теоретических методов и с экспериментальными данными [25] дает хорошее качественное и вполне удоветворительное количественное совпадение.

В вышеупомянутой работе Османа метод ЯЯ-линеаризации не получил строгого обоснования. В работе П. П. Мостовенко [41 ] показано, что этот метод, который заключается в замене нелинейного уравнения Рейнольдса его упрощенной математической моделью - уравнением, линейным относительно функции ¥ = = РН, эквивалентен линеаризации уравнения Рейнольдса с помощью обычного метода малого параметра в первом приближении, если в этом уравнении предварительно перейти к новой искомой функции

Метод РЯ-линеаризации можно интерпретировать и с позиций функционального анализа. Для определенности рассмотрим уравнение Рейнольдса (3.20), соответствующее цилиндрическому подшипнику; сделаем подстановку

= 1 (3.41) тогда уравнение (3.20) запишется в виде

R (¥, Я) = [¥ (¥фЯ- ¥Яф)]ф +

+ 0[¥(¥5Я-¥ЯО]£-хП- = О. (3.42)

Здесь и далее штрихи и подстрочные индексы ф, обозначают частные производные по соответствующим координатам, точка - производную по времени.

Уравнение (3.42) представляет собой квазилинейное уравнение параболического типа. Если его левую часть R (Y, Я) рассматри 84

вать как функцию независимых переменных ф (ф, 1, т), то соотно-

R(,H)0 (3.43)

можно трактовать как осуществляемое оператором R отображение банахова пространства функций ¥} X \Н], где Я - заданный, а искомый элемент этого пространства, в другое банахово пространство Ф} [24].

Применим к уравнению (3.42) обобщенный метод Ньютона - Канторовича [21, 24], согласно которому искомое решение аппроксимируется последовательностью функций:

Wn+i = - {R (¥ , Я)]-1 R (Ч, Я), (3.44)

где R {¥п, Я) - сильная производная оператора R в точке банахова пространства; {R (¥ , Н)]- - обратный оператор; п = О, 1, 2, ... Как показано в [24], процесс последовательных приближений, определяемый рекуррентной системой уравнений (3.44), может быть заменен другим, более удобным с вычислительной точки зрения

n.i = - \.R (0, Яо)]-1 R {а, Н). (3.45)

Эта формула отличается от предыдущей тем, что на каждой итерации обратный оператор [i? (¥а, Яо) 1 определяется в одной и той же точке ¥о банахова пространства при фиксированном значении Я = Яо-

Примем в качестве исходной точки ¥о = 1 при Яо= 1-В нашем случае оператор R (¥, Я) имеет сильный дифференциал (дифференциал Фреше), который в рассматриваемой точке можно определить по формуле

/(Уо.Яо) ==Ит + -.°- (3.46)

как операцию над элементом и банахова пространства, где % - числовой параметр. Учитывая структуру оператора R в уравнении (3.42) и производя дифференцирование, получим

R (Чо, Яо) и = фф + o4ii~ilHoU:, - u. (3.47)

Положив далее в уравнении (3.45) = 0; ¥о=1; Яо=1 и применив к нему оператор (3.46), найдем

Rio, Но) Wi = R {Wo, Но) (D-R {Wo, Я). >

Учитывая, что R {Wq, Яо)(1) = О, используя выражения (3.47) и (3.42) при 40 = 1

R{Wo, Я)=-(Яфф+оЯЕ£),

(¥,)фф + о {Wi)k -7Л1)ф-*> = + (-

получим

Таким образом, определение 1-го приближения по схеме модифицированного метода Ньютона-Канторовича сводится к решению линейного неоднородного дифференциального уравнения параболического типа (3.48) при соответствующих граничных и начальных условиях. Это уравнение и есть РЯ-линеаризованное уравнение Рейнольдса, полученное впервые Османом.

Уравнения второго и последующих приближений могут быть найдены аналогично; так, во втором приближении будем иметь

(Ч2)фф + сг= (2)Ее- X (42);-Ч>2 - Яф + аЩ--R(W,H).

(3.49)

Сходимость процесса последовательных приближений, описываемого уравнением (3.45), зависит от выбора начальных элементов Wq, Но, а также от свойств функции Я (ф, С, т). Здесь сошлемся на теорему, которая приводится в монографии [24]. С незначительными изменениями в формулировке эта теорема действует и в данном случае.

Все вышеизложенное применимо также к основному уравнению газовой смазки в сферических, полярных, конических координатах; например, уравнение (3.11) для сферического подшипника подстановкой (3.41) приводится к виду

R(W, Я) = [WiWH - WH)r + s\ne[siaQ-Y{%H~4He% -

- XSitf е-; -sin=e-t = 0. (3.50)

В этом случае дифференциал Фреше (3.46) равен при = = Яо = 1

R (Wo, Но) и = мфф + sin 8 (sin 8 ивУв - sin 8 {%и + и).

(3.51)

Соответствующие РЯ-линеаризованные уравнения 1 и 2-го приближений, аналогичные уравнениям (3.48) и (3.49), можно представить в виде:

R(Wo,Ho)W,Q{<p,Q,x); (3.52)

R (¥о. Но) W, = Q (ф, 8, т) - Р (¥i. Я). (3.53)

Левые части уравнений (3.52) и (3,53) получаются из (3.51) заменой и на или W, функция р - из (3.50) (W W,), а функция Q равна

С-Я;ф + 81пе(51п9-Яе)Ь. Сделаем теперь одно важное для дальнейшего анализа замечание, которое касается уточнения решения РЯ-линеаризованной задачи. Хотя решение уравнения 1-го приближения (для Wi) может быть представлено в конечном виде, но оно получается довольно сложным, что затрудняет вычисление поправочного члена Р (Ti, Я) в правой части уравнения 2-го приближения. В связи с этим может оказаться более целесообразной коррективе

ровка 1-го приближения с помощью аддитивной или какой-либо иной поправки, не противоречащей граничным условиям задачи.

Такая корректировка особенно проста, если задача стационарна (заданные и искомые функции не зависят от времени) и ее решение удовлетворяет условию периодичности по одной из координат, например условию (3.14). В частности, для цилиндрического подшипника стационарное решение 1-го приближения Wi (ф, $), имеющее период 2я по координате ф, можно уточнить с помощью аддитивной поправки Д (Q

Ч. = 1(Ф. S) + A(S)-

(3.54)

Подставляя W вместо W в (3.49), полагая там - О и почленно интегрируя его по ф в пределах от О до 2я, получим:

Ак = - j Р (41, Я) ф. (3.55)

Подынтегральная функция в (3.55) вычисляется на основании решения стационарного уравнения 1-го приближения, которое

получается из (3.48) при = 0.

Другой способ вычисления поправочного члена А (Q может быть основан на методе Галеркина-Канторовича [22], согласно которому дифференциальное уравнение для А получается из условия ортогональности

P(4i-f А, Я) Ф-О.

(3.56)

При корректировании нестационарных решений 1-го приближения необходимо учитывать зависимость поправки от времени. Если краевые условия по-прежнему допускают аддитивную поправку А (g, т) в виде (3.54), то вместо обыкновенного дифференциального уравнения (3.55) будем иметь уравнение в частных производных

oAl-A = ~-±-R(WuH)d, (3.57)

правая часть которого - известная функция t, и х.

Метод РЯ-линеаризации дает возможность найти решение уравнения Рейнольдса, а вместе с ним и зависимости реакций газодинамических подшипников от смещений шипа в удобной аналитической форме, что значительно упрощает исследование динамики ротора (гл. V, VI). Однако ввиду нелинейного характера упомянутых зависимостей иногда целесообразно прибегать к их линеаризации, ограничиваясь случаем малых колебаний ротора,