щейий, получим

PaRL

- 1б(б+£) Р) Я (ж + i-ol о (5-31)

(S)

Интегрирование здесь производится по всей несущей поверх-, ности s: -О < ф 2n. Формула (5.31) по своей структуре аналогична формуле (5.18), но в данном случае она представляет реактивный момент смазочной пленки подшипника, возникающий npjj угловых колебаниях шипа вокруг центральной точки О.

Таким образом, реакция цилиндрического подшипника на угловые смещения (без учета поступательных), как и реакция на поступательные смещения, представляется с помощью двух передаточных функций в виде, аналогичном (5.18).

Для периодического профиля с периодом 2п/п {п 3) при малых колебаниях в окрестности среднего положения формула (5.31) упрощается так же как и в (5.18), второй интеграл в (5.31) обращается в нуль.

Напомним, что результаты этого и предыдущего параграфов получены обобщенным методом РЯ-линеаризации в первом приближении. Заметим, что во втором приближении поправки могут быть найдены методом гармонического баланса либо из уравнения (3.57), либо непосредственно из уравнения Рейнольдса. В последнем случае объем вычислений резко возрастает и требует применения вычислительной техники.

23. Исследование поступательных колебаний ротора в газодинамических подшипниках в первом приближении

Результаты, полученные в предыдущих параграфах, можно непосредственно применить к исследованию поступательных и угловых колебаний ротора в профилированных подшипниках с газовой смазкой.

Рассмотрим машину с обращенным ротором и вентилируемыми подшипниками. В качестве примера такой машины может служить гироскоп катушечного типа. Вентиляционные каналы служат для улучшения обмена смазочной среды и одновременно обеспечивают независимость течения смазки в радиальном и упорном подшипниках.

Рассмотрим вначале поступательные колебания ротора при жестко закрепленном статоре. Профилированная поверхность

(шевронные каНавки) предполагаемся неподвижной, а ЁраЩаЮ-щаяся - гладкой.

Положение ротора при чисто поступательных колебаниях

можно определить вектором смещения е. Согласно сказанному в гл. II эти колебания можно разделить на осевые и радиальные, так как они в первом приближении независимы.

Оставляя в стороне осевые колебания, рассмотрим только радиальные. Мгновенное положение ротора при радиальных колебаниях удобно определить комплексным вектором = 8j + ге,

-; б-минимальный зазор при централь-

!l

ном положении ротора; Е - половина глубины канавки.

Запишем уравнение малых радиальных колебаний ротора в вариациях; согласно (2.10)

(б + £) М A8i = Af 1-f Af 1в, (5-32)

где М -масса ротора; Afi = Afj + tAf - комплексная сила реакции подшипника; Af ib - Af + iAf- комплексная возмущающая сила; точки обозначают дифференцирование по времени t.

Переходя в этом уравнении к безразличному времени т = г, получим

43(

(8-}-Е)М Ael = Af 1 + Af ib.

(5.33)

Штрихи здесь обозначают дифференцирование по безразмерному времени т.

Если внешние возмущения не зависят от времени, т. е. f 1в = fiB = const,

имеем уравнение

(8 + Е)М АеГ = Af 1,

(5.34)

которое соотвегствуег случаю малых свободных колебаний ротора около положения равновесия, смещенного относительно центра подшипника (ею ф 0) при fiB 0.

Предположим теперь, что начальные условия нулевые и FIb = О, но Afi>B ф О, т. е. рассмотрим случай вынужденных поступательных колебаний ротора около центрального положения равновесия t8io = 0).

Преобразуя уравнение (5.33) по Лапласу и подставляя Afj из (5.19), найдем

PaRL

(5.35) 125

учитывая (5.14), получим!

Re (Xol = 4a = const;

Первый интеграл в общем виде выражается довольно сложно, поэтому рассмотрим его асимптотическое значение при < 1, Для достаточно длинного подшипника имеем:

efs.O

(s)~l;

Рис. 27

G(S, О

Тогда асимптотическое представление

-а+Ь

(5.36)

Здесь а и b - постоянные коэффициенты, которые вычисляются на основе стационарного решения краевой задачи для центрального положения ротора.

Для исследования колебаний и устойчивости применим частотный метод Михайлова-Найквиста. Рассмотрим эквивалентную одноконтурную систему автоматического регулирования [29], представленную для полученных уравнений на рис. 27.

Передаточная функция разомкнутой цепи эквивалентного контура с обратной связью с учетом (5.35) и (5.36) будет

(5.37)

гле X -JM+IL-

G(s, i) = a-i-b.p. Полагая s = ш и задавая значения со в пределах от -оо до +00 построим амплитудно-фазовую частотную характеристику lilrrL rh представляющую собой годограф комплексного вектора и на комплексной плоскости с

Оказывается, что в зависимости от соотношения параметров, возможны два случая, построенные на рис. 28: а - устойчивость при a/XgQ > 1; б - неустойчивость при а/Х < 1.

Таким образом, получаем условие устойчивости в виде

4paRL а

1 <

(5.38)

Обратим внимание на то, что в условие (5.38) не входит коэффициент b и, кроме того, это условие не зависит от замены W (s, 1, i)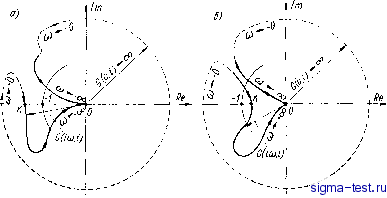

Рис. 28

приближенным асимптотическим выражением. Это значит, что условие (5.38) справедливо и при больших значениях параметра Сто = D/L.

Учитывая выражение для коэффициента а, перепишем (5.38) в следующем виде:

AfQa (б + Е) PaRL

<4а= {{-Re {Жо\ йф dl. (5.39)

Это условие полностью согласуется с критерием устойчивости по А. С. Шейнбергу [58], а также с результатами работы ПО]. Невыполнение этого условия приводит к возникновению неустойчивости типа полускоростного вихря. При этом ротор, вращаясь вокруг своей оси с угловой скоростью Q, начинает совершать орбитальное движение по расходящейся спирали с угловой скоростью близкой к Й/2.

Как уже отмечалось выше, явление полускоростного вихря в случае использования гладких подшипников было хорошо изучено в работах А. С. Шейнберга и других авторов [54, т. 87, № 1 ]. Оно являлось долгое время препятствием широкому распространению газодинамических подшипников. Только в последнее

время было выяснено, что в легконагруженных машинах для обеспечения устойчивости необходимо применять профилированные подшипники 154, т. 86; 46, т. 90, № 4]. Перепишем условие (5.39) в другом виде

PaRL

(5.39)

В таком виде левая и правая части имеют размерность жесткости. Можно показать, что правая часть (5.39) выражает среднюю по времени радиальную жесткость подшипника при малом смещении шипа из центрального положения вдоль линии центров, в режиме орбитального движения с угловой скоростью, равной Q/2. Левая часть (5.39) представляет собой величину градиента центробежной силы, обусловленной орбитальным движением ротора, масса которого считается сосредоточенной в его центре. Назовем правую часть (5.39) вихревой жесткостью , тогда условие (5.39) можно сформулиров.ать следующим образом.

Для асимптотической устойчивости уравновешенного ротора в центральном положении при жестко закрепленных подшипниках необходимо, чтобы градиент центробежной силы был меньше средней вихревой жесткости подшипников.

Следует заметить, что оценка вихревой жесткости по формул-е (5.39) является приближенной, так как эта формула получена на базе краевой задачи в 1-ом приближении. Более точно вихревую жесткость можно рассчитать, исходя из, нелинейного уравнения Рейнольдса. К этому надо добавить, что определение самого понятия вихревой жесткости требует уточнения. Дело в том, что угловая скорость- орбитального движения, соответствующего порогу неустойчивости, может несколько отличаться от значения QJ2: Более точно угловая скорость орбитального движения на пороге неустойчивости определяется из условия обращения в нуль средней за период тангенциальной составляющей главного вектора всех сил, действующих на вал ротора со стороны смазочной пленки.

Возвращаясь к частным характеристикам, обратим внимание на то, что они дают возможность определить другие важные динамические характеристики подшипников с газовой смазкой. Например, динамическая жесткость при гармонической вибрации основания с частотой со будет выражаться комплексным вектором 1 + Go (ш, i).

Амплитуда синхронного вихря при наличии статического дисбаланса может быть определена через модуль динамической жесткости I 1 + Go (2tXo. О . вычисленной при частоте со = 2хо, соответствующей угловой скорости вращения ротора fi.

Все динамические характеристики, найденные в 1-м приближении, могут быть*уточнены во 2-м приближении методом гармо-ническогобаланса.

24. Исследование угловых колебаний ротора в газодинамических подшипниках

Кроме поступательных радиальных колебаний, рассмотренных выше, ротор может совершать угловые колебания. Эти колебания могут совершаться одновременно с радиальными, но, учитывая сказанное в гл. II и предполагая, что перекрестные связи малы, рассмотрим отдельно угловые колебания. Рассмотрим снова мо-, дель машины (гироскопа) с обращенным ротором в профилирова-ных цилиндрических подшипниках (см. рис. 17). Для простоты предположим, что влиянием упорных пластин можно пренебречь (можно показать, что они влияют на количественные оценки).

Предполагая еще, что ротор вращается с постоянной угловой скоростью Й и совершает малые угловые колебания, запишем дифференциальные уравнения в форме одного комплексного уравнения (2.19)

/ Ш - iKo AU = - iASi - i ASiB-

(5.40)

Здесь At/ = АХ + iY - комплексная координата; Ко - кинетический момент; ASi = А + 1Ац - комплексный вектор момента сил, действующих на ротор со стороны смазочного слоя; ASiB = Д2в + iSrB - комплексный вектор момента внешних возмущающих сил.

Это уравнение эквивалентно двум линейным уравнениям, описывающим малые угловые колебания гироскопа вокруг неподвижной точки.

Для случая малых углов а АХ; AY момент сил реакции смазочной пленки согласно (5.31) будет равен (в изображениях по Лапласу)

PaRL

16(6 + Е)

Ш J j (+ -i Re \Жо\ l) ац> (5.41)

Напомним, что формула (5.41) справедлива для подшипника с периодическим профилем при л 3 (см. п. 20). Поступая так же, как и в п. 23, перейдем в уравнении (5.40) к безразмерному времени и преобразуем его по. Лапласу по аналогии с уравнением (5.32)

Q2 - . Q

§2 Д/ if(

sAU= - iASi - iASi

(5.42)

Здесь начальные условия, как и ранее, приняты нулевыми. Обозначая далее

О. (s О = -TeW \\{ + 4гто d (5-43)

9 в. Н . Дроздсвнч